La semplificazione delle frazioni è un passaggio fondamentale in matematica.
Permette di rendere una frazione più semplice mantenendone invariato il valore.
Questa competenza è essenziale per risolvere problemi, sommare o moltiplicare frazioni.
In questa lezione vedremo:
- Che cos’è una frazione? (con una presentazione del numeratore e del denominatore).
- Cosa significa semplificare una frazione, con una definizione chiara e concisa.
- Un metodo semplice per semplificare una frazione, spiegato passo dopo passo.
- Esempi concreti per illustrare ogni passaggio.
- Consigli pratici per riconoscere rapidamente se una frazione può essere semplificata.
L’obiettivo è fornire ai bambini (e ai genitori) gli strumenti per padroneggiare questo concetto chiave della matematica.
Che cos’è una frazione?
Una frazione è un modo per rappresentare una parte di un intero o per esprimere un rapporto tra due quantità. È composta da due elementi:
- Il numeratore: il numero scritto sopra la linea di frazione, che indica quante parti sono considerate.
- Il denominatore: il numero scritto sotto la linea di frazione, che indica in quante parti uguali è diviso l’intero.
Esempio:
La frazione \frac{3}{4} significa che un oggetto (o una quantità) è diviso in 4 parti uguali e che se ne prendono 3.
Illustrazione:
Se hai una pizza tagliata in 4 fette uguali e ne mangi 3, hai consumato \frac{3}{4} della pizza.
Perché imparare a semplificare una frazione?
Semplificare una frazione significa ridurre i due termini (numeratore e denominatore) mantenendo invariato il loro valore. È un modo per rendere la frazione più facile da comprendere e da utilizzare.
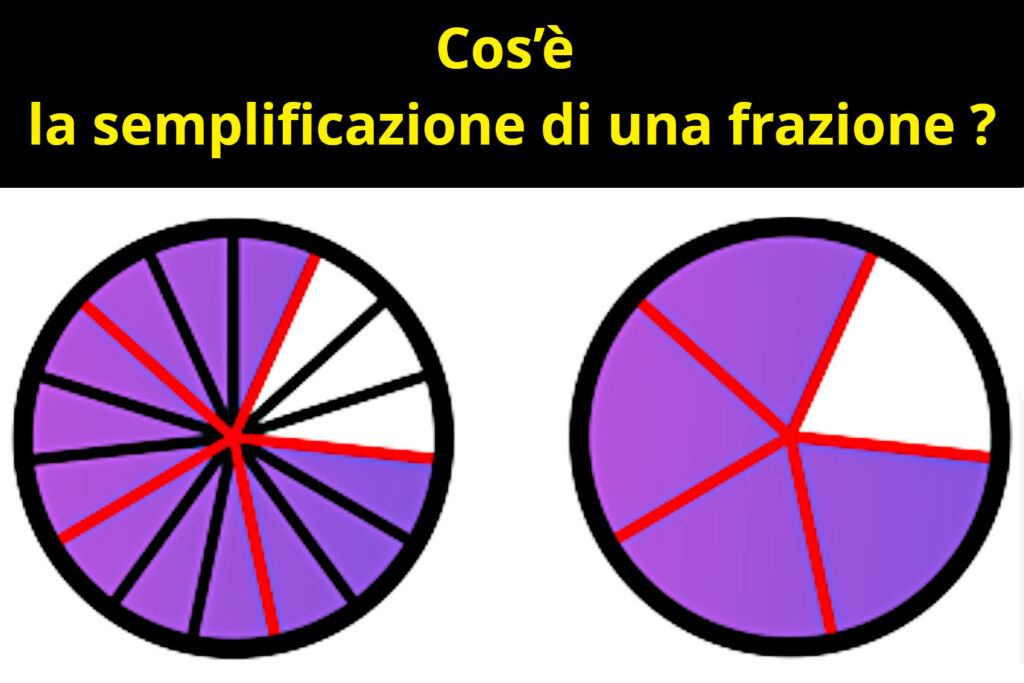
Che cos’è la semplificazione di una frazione ?
Semplificare una frazione significa riscriverla in una forma più semplice dividendo il numeratore (il numero sopra) e il denominatore (il numero sotto) per il loro massimo comune divisore (MCD). La frazione semplificata è più semplice da manipolare ma rimane equivalente a quella iniziale.
Esempio:
La frazione \frac{6}{9} può essere semplificata in \frac{2}{3}, poiché 6 e 9 hanno un divisore comune: 3.
Metodo per semplificare una frazione
Passaggio 1: Identificare l’MCD del numeratore e del denominatore
Il MCD (Massimo Comune Divisore) è il numero più grande che divide sia il numeratore che il denominatore.
Come calcolare il MCD (Massimo Comune Divisore)?
Esistono diversi metodi per calcolare il MCD, ma uno dei più semplici consiste nel fare l’elenco dei fattori del numeratore e del denominatore e cercare il numero più grande che è comune a entrambi.
Esempio:
Per la frazione \frac{12}{8}, i divisori di 12 sono: 1,2,3,4,6,121, 2, 3, 4, 6, 12
I divisori di 18 sono: 1,2,3,6,9,181, 2, 3, 6, 9, 18
Il massimo comune divisore è 6.
Passaggio 2: Dividere il numeratore e il denominatore per l’MCD
Una volta identificato l’MCD, dividi numeratore e denominatore per questo numero.
Esempio:
\frac{12}{18}/ 6 = \frac{2}{3}
La frazione semplificata è quindi \frac{2}{3}.
Passaggio 3: Verificare se la frazione è effettivamente semplificata
Una frazione è semplificata se numeratore e denominatore non hanno più divisori comuni (eccetto 1).
Esempio: In \frac{2}{3}, l’unico divisore comune tra 2 e 3 è 1. La frazione è quindi semplificata.
Esempi Pratici di semplificazione di frazione
- Semplificare \frac{8}{12} :
- Divisori di 8: 1,2,4,81, 2, 4, 8
- Divisori di 12: 1,2,3,4,6,121, 2, 3, 4, 6, 12
- MCD = 4.
- \frac{8}{12}/4 = \frac{2}{3}.
- Semplificare \frac{15}{25} :
- Divisori di 15: 1,3,5,151, 3, 5, 15
- Divisori di 25: 1,5,251, 5, 25
- MCD = 5.
- \frac{15}{25}/5 = \frac{3}{5}.
Consigli per semplificare le frazioni più velocemente
- Utilizza i criteri di divisibilità:
- Se entrambi i numeri sono pari, dividi per 2.
- Se entrambi i numeri terminano con 0 o 5, dividi per 5.
- Semplificazione progressiva: Se non trovi subito l’MCD, dividi progressivamente per piccoli numeri comuni (2, 3, 5, ecc.).
Esempio: Per 4860\frac{48}{60} :
- Dividi prima per 2: \frac{48}{60}/2 = \frac{24}{30}.
- Dividi ancora per 2: \frac{24}{30}/2 = \frac{12}{15}.
- Infine, dividi per 3: \frac{12}{15}/3 = \frac{4}{5}.
La semplificazione delle frazioni nelle situazioni quotidiane
La semplificazione delle frazioni non è solo un concetto matematico astratto, ma può essere utilizzata in molte situazioni pratiche quotidiane. Ecco quelques exemples :
- Dividere un pasto:
Immagina di essere a tavola con la tua famiglia e di voler dividere una pizza in parti uguali. Se la pizza è divisa in 8 fette e ne mangi 6, la frazione è \frac{6}{8}. Tuttavia, semplificandola, otteniamo \frac{3}{4}, che è più facile da comprendere. - Fare una ricetta:
In cucina, le frazioni sono spesso usate per misurare gli ingredienti. Se una ricetta richiede \frac{4}{6} di una tazza di zucchero, semplificando la frazione otteniamo \frac{2}{3}, che è più semplice da usare quando misuri gli ingredienti. - Condivisione di oggetti:
Quando si deve dividere qualcosa tra amici, la semplificazione delle frazioni può rendere più facile capire quante parti si ottengono. Ad esempio, se 12 persone devono condividere una torta e ognuna riceve \frac{12}{16} della torta, semplificando la frazione otteniamo \frac{3}{4}, che è più intuitivo.
Note per i genitori: Questi esempi mostrano ai bambini come la semplificazione delle frazioni possa essere utile per risolvere problemi della vita quotidiana in modo più rapido e comprensibile.
Potreste anche incoraggiare gli studenti a provare a semplificare le frazioni che incontrano nella loro vita quotidiana, come quelle legate alle attività in cucina, alla condivisione di giochi o persino alla misurazione di distanze.
Conclusione sulla semplificazione delle frazioni
La semplificazione delle frazioni è una competenza fondamentale che semplifica i calcoli e aiuta a comprendere meglio le frazioni. Con questo metodo, i bambini possono esercitarsi a riconoscere i divisori comuni e a manipolare le frazioni con sicurezza.
Per esercitarti di più, esplora i nostri Esercizi sulla Semplificazione delle Frazioni e torna presto per scoprire nuovi contenuti didattici gratuiti!
Domande Frequenti sulla Semplificazione delle Frazioni
1. Cos’è il Massimo Comune Divisore (MCD)?
Il Massimo Comune Divisore (MCD) è il numero più grande che divide entrambi i numeri di una frazione senza lasciare resto.
Ad esempio, per la frazione \frac{12}{8}, l’MCD è 4.
2. Come si calcola il MCD?
Esistono diversi metodi per calcolare il MCD. Uno dei più semplici consiste nel trovare tutti i divisori di entrambi i numeri e scegliere il più grande numero che è comune a entrambi.
3. Come posso sapere se una frazione può essere semplificata?
Una frazione può essere semplificata se il numeratore e il denominatore hanno almeno un divisore comune maggiore di 1. Se non hanno divisori comuni, la frazione è già nella sua forma più semplice.
4. Quando una frazione è completamente semplificata?
Una frazione è completamente semplificata quando il numeratore e il denominatore non hanno altri divisori comuni, tranne il numero 1.
5. Posso semplificare tutte le frazioni?
No, non tutte le frazioni possono essere semplificate. Se il numeratore e il denominatore sono numeri primi tra loro (ovvero, hanno come unico divisore comune il 1), la frazione non può essere ulteriormente semplificata.
6. Cosa devo fare se non riesco a trovare l’MCD?
Puoi semplificare progressivamente. Prova a dividere il numeratore e il denominatore per numeri più piccoli (ad esempio, 2, 3, 5) fino a trovare un divisore comune.
7. Posso usare una calcolatrice per semplificare le frazioni?
Sì, puoi usare una calcolatrice per calcolare il MCD, ma è importante anche comprendere il processo manuale per sviluppare una buona comprensione della semplificazione delle frazioni.
8. A che classe si apprende la semplificazione delle frazioni?
La semplificazione delle frazioni è un concetto che viene introdotto di solito nella scuola primaria, a partire dalla classe quarta o quinta. Tuttavia, può essere ripreso e approfondito anche nelle classi successive, come nella scuola media.
9. La semplificazione delle frazioni è utile nella vita di tutti i giorni?
Sì, la semplificazione delle frazioni è utile in molte situazioni quotidiane.
Ad esempio, può aiutarti a fare calcoli più veloci quando dividi oggetti in parti uguali (come torte o pizze), o quando devi risolvere problemi legati a misurazioni, come nel caso di ricette o progetti che richiedono frazioni.
Per qualsiasi altra domanda, non esitare a lasciare un commento o consultare gli esercizi pratici disponibili sul nostro sito!